前回に引き継いでもう少し問題の方をやってみようかと思います。

5年生の割合とグラフです。（僕は全問中、半分間違っていました。）

 

割合とグラフは結構つまづきやすいのではないでしょうか。

公式に

割合＝くらべられる量÷もとにする量

というのがありますが、この意味を理解できていなければ公式を丸ごと覚えたとしても分からないのは当然かと思います。

僕が間違えた問題を全部ここで述べます。

問1　小数を百分率に直しなさい（○○のところ）

小数1.8＝百分率○○

これは、単に100をかければいいだけです。小数に100をかけると百分率になります。

よって180％

です。簡単ですね。（といいながら、なぜか自分は1800にしてしまった・・・）

 

問2　□に当てはまる数を書きましょう

①　□円は、1200円の30％である。

言い直すと、1200円を0.3でかけるといくつですか?

という問題になります。

くらべられる量。要は小数を掛けた結果が□なんですね。

(くらべられる量＝小数を掛けた値＝もとにする量より小さい値）

答えは　1200×0.3=360(円)

です。

□＝360円　はもとにする量1200円より少ないですね。

 

 

②　110gは□gの55％です。

□を55％（0.55）かけると110gになるという言い方ですね。

この問題では、□はもとにする量になります。

よって、

もとにする量×割合＝くらべられる量（こっちの方が僕は分かりやすい）

ので、

もとにする量＝くらべられる量/割合

に変換して

□＝110g/0.55

で答えは200gですね。

200gのもとにする量は110gのくらべられる量より大きいですのであってます。

 

③　8000㎡の70％は□㎡です。

今まで、主語がくらべられる量の問題だったため、流れで、8000㎡もくらべられる量だ!

なんて考えないように気をつけましょう。（それを狙っているかも）

 

8000㎡を70％（0.7）でかけると□㎡

なので

8000×0.7=5600(㎡)

ですね。

8000はもとにする量。5600はくらべられる量ですので、大小関係は大丈夫そうですね。

 

問3　5年生の120人の好きな食べ物の割合を下のような帯グラフで表しました。

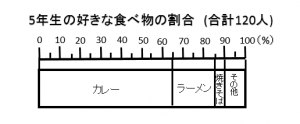
①　ラーメンが好きな人の割合は何％ですか

表を見ると65～85％がラーメンの割合ですね。

答え　20％

②　カレーが好きな人は何人ですか

表を確認するとカレーは65％いますね。

これにもとにする量をかければOKです。（もとにする量×割合＝くらべられる量）

よって合計が120人なので

120×0.65=78(人)

ですね。

表の数値を間違えないように気をつけましょう。

帯グラフに続いて円グラフですが、円グラフを書くときの注意が

大きい割合からまず先頭に書く（その他は一番最後）

ことです。表をもとに割合を円グラフに書く問題でよくやってしまうのが、

表の順番に円グラフも順番に割合を書いてしまう

ことがあるため、表の項目の中で一番割合が多い項目から順に円グラフを0から書いていくのが常識です。

 

当時、僕もそれで間違えてしまったのでその点も気をつけましょう。

 

でも、今はExcelで一発でグラフにできるから便利ですよね。

[ad#lower1]